加密货币曲线图解法,洞察市场波动与投资策略

你有没有想过，那些神秘的加密货币，它们是如何在数字世界中安全地穿梭的呢？今天，就让我带你一起揭开加密货币曲线图解法的神秘面纱，让你对这些数字宝藏有更深入的了解。

一、曲线图解法：加密货币的守护神

想象加密货币的世界就像一个巨大的迷宫，而曲线图解法就是那把开启迷宫大门的钥匙。它是一种基于数学原理的加密技术，为加密货币的安全保驾护航。

二、什么是曲线图解法？

曲线图解法，也就是椭圆曲线密码学（ECC），是一种特殊的数学曲线。它由一系列满足特定方程的点组成，这些点构成了一个特殊的数学结构——椭圆曲线。

三、曲线图解法的特点

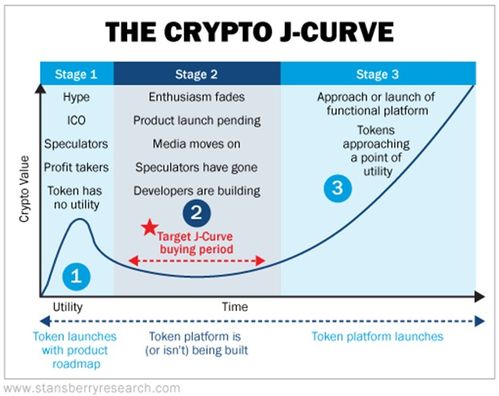
1. 安全性高：与传统的加密算法相比，曲线图解法在相同密钥长度下，安全性更高。这是因为椭圆曲线上的运算具有特殊的数学性质，使得破解难度大大增加。

2. 计算效率高：曲线图解法在计算上具有更高的效率，可以更快地完成加密和解密操作。

3. 存储空间小：由于密钥长度较短，曲线图解法所需的存储空间更小，这对于移动设备和区块链等应用来说尤为重要。

四、曲线图解法在加密货币中的应用

1. 密钥生成：曲线图解法用于生成公钥和私钥。用户通过私钥可以生成对应的公钥，公钥用于接收比特币，私钥用于签名交易。

2. 签名验证：曲线图解法用于验证交易签名。当用户发送比特币时，需要使用私钥对交易进行签名，接收方可以通过公钥验证签名的有效性。

3. 地址生成：比特币地址是由公钥生成的，公钥经过一系列转换后得到比特币地址，用于接收和发送比特币。

五、曲线图解法的数学原理

1. 椭圆曲线上的点加法：对于椭圆曲线上的两个点P和Q，它们的和为R，可以通过以下公式计算：R (x3, y3)，其中x3 (2x1x2 + a) / (x1 - x2)^2，y3 (y1 - y2 (x1 - x2)^-1) (x1 - x2)^-3。

2. 椭圆曲线的乘法：对于椭圆曲线上的一个点P和整数n，P的n倍为Q，可以通过以下公式计算：Q (x3, y3)，其中x3 (n^2x - nx1 - x2) / n^3，y3 (n(x1 - x2) x3 - y1) / n^3。

3. 椭圆曲线的逆元：对于椭圆曲线上的一个点P，其逆元为P'，可以通过以下公式计算：P' (x', y')，其中x' (x^3 + ax + b) / (2y)，y' (y^3 + ax2 + bx + c) / (2y)。

六、曲线图解法的未来

随着加密货币的不断发展，曲线图解法在加密货币领域的应用将越来越广泛。未来，我们可以期待曲线图解法在区块链、物联网、云计算等领域的更多应用。

曲线图解法作为加密货币的守护神，为我们的数字世界带来了安全与便捷。让我们一起期待，这个神秘的数学世界，为我们带来更多的惊喜吧！