比特币方程是什么,揭秘数字货币的数学基础

比特币方程：揭秘数字货币的数学基础

比特币，作为一种革命性的数字货币，其背后有着复杂的数学原理。本文将深入探讨比特币方程的奥秘，揭示其作为数字货币的数学基础。

一、比特币方程的起源

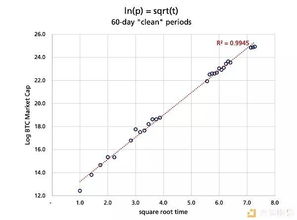
比特币方程的起源可以追溯到2008年，当时一位化名为中本聪的匿名人士发布了比特币的白皮书。在这份白皮书中，中本聪首次提出了比特币的概念，并详细阐述了比特币的工作原理。比特币方程作为比特币的核心，承载了比特币的安全性和去中心化特性。

二、椭圆曲线方程在比特币中的应用

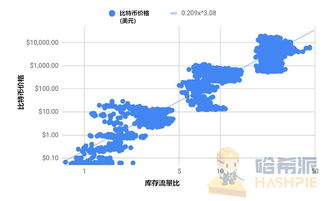
比特币方程的核心是椭圆曲线方程。椭圆曲线方程是一种特殊的数学方程，它在比特币的加密算法中扮演着至关重要的角色。比特币使用的椭圆曲线方程是secp256k1，这是一种基于有限域数学的椭圆曲线。

椭圆曲线方程的一般形式为：y2 = x3 + ax + b，其中a和b是常数。在比特币中，secp256k1椭圆曲线方程被定义为y2 = x3 + 7x + 0。这种方程的数学特性使得比特币的加密算法具有很高的安全性。

三、比特币方程的安全性

比特币方程的安全性主要得益于椭圆曲线密码学。椭圆曲线密码学是一种基于椭圆曲线数学的密码学，它利用了椭圆曲线上的离散对数问题来保证加密算法的安全性。在比特币中，椭圆曲线密码学被用于生成公钥和私钥，以及进行数字签名。

由于椭圆曲线密码学的复杂性，使得破解比特币方程变得极其困难。这使得比特币在交易过程中具有很高的安全性，有效防止了欺诈和篡改。

四、比特币方程的数学原理

比特币方程的数学原理主要涉及以下几个方面：

椭圆曲线上的点加法：在椭圆曲线上，任意两个点P和Q的和可以表示为另一个点R，满足R = P + Q。

椭圆曲线上的点倍：在椭圆曲线上，一个点P的倍数可以表示为另一个点Q，满足Q = 2P。

离散对数问题：在椭圆曲线上，给定一个点P和它的倍数Q，找到整数k使得Q = kP是一个困难的问题。

这些数学原理共同构成了比特币方程的基础，为比特币的安全性和去中心化特性提供了保障。

五、比特币方程的应用

比特币方程的应用非常广泛，主要包括以下几个方面：

生成公钥和私钥：比特币方程可以用于生成用户的公钥和私钥，这是比特币交易的基础。

数字签名：比特币方程可以用于生成数字签名，确保交易的安全性。

工作量证明：比特币方程在比特币的挖矿过程中扮演着重要角色，用于验证交易并生成新的区块。

比特币方程的应用使得比特币成为一种安全、可靠、去中心化的数字货币。

比特币方程作为数字货币的数学基础，承载了比特币的安全性和去中心化特性。通过对椭圆曲线方程、离散对数问题等数学原理的应用，比特币方程为比特币的广泛应用提供了保障。随着数字货币的不断发展，比特币方程的研究和应用将越来越受到重视。