比特币曲线属性,比特币曲线属性解析

比特币曲线属性解析

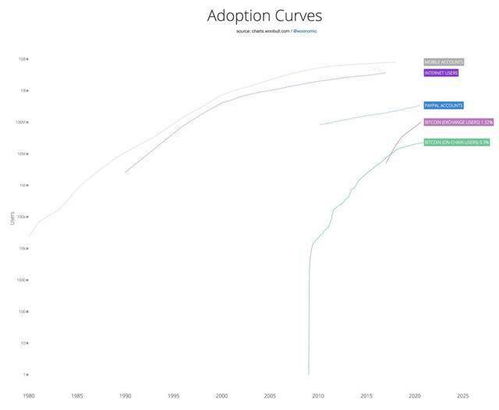
随着区块链技术的不断发展，比特币作为最早且最成功的加密货币，其背后的数学原理和曲线属性引起了广泛关注。本文将深入解析比特币曲线的属性，帮助读者更好地理解这一加密货币的核心技术。

一、比特币曲线概述

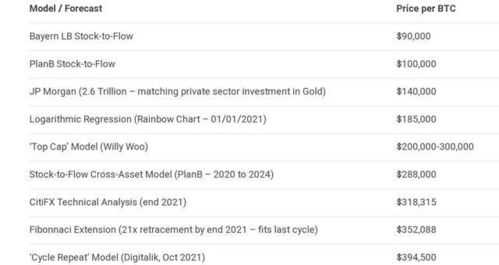
比特币曲线，即椭圆曲线，是一种特殊的数学曲线，具有独特的数学性质。在比特币系统中，椭圆曲线被用于公钥和私钥的生成、数字签名以及交易验证等关键环节。

二、比特币曲线的参数

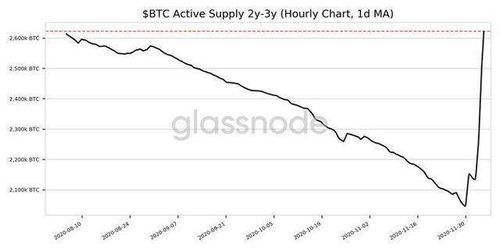
比特币曲线的参数包括系数a、b、p、G和n。其中，a和b是椭圆曲线的系数，p是有限域的质数，G是生成元，n是椭圆曲线的阶。

在比特币中，a和b的值分别为0和7，p的值为0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141，G的x坐标为0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798，y坐标为0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8，n的值为0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAaedce6af48a03bbfd25e8cd0364141。

三、比特币曲线的生成元

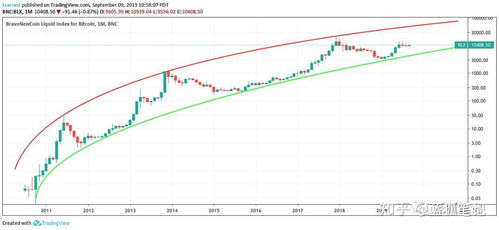
生成元G是椭圆曲线上的一个特殊点，通过不断将G乘以整数，可以生成一个群，直到它转化为单位点。在比特币中，n值使得nG是单位点，其值为0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAaedce6af48a03bbfd25e8cd0364141。

生成元G的选择对于比特币的安全性至关重要。如果生成元G的选择不当，可能会导致比特币系统的安全隐患。

四、比特币曲线的私钥和公钥

在比特币中，私钥是一个随机生成的64位整数，用于生成公钥。私钥k与公钥K之间的关系为K = kG。公钥K是公开的，而私钥k是保密的。

私钥和公钥的生成过程如下：

选择一个随机数k（0

计算公钥K = kG。

五、比特币曲线的数字签名

数字签名是比特币交易验证的关键环节。在比特币中，数字签名是通过椭圆曲线离散对数（ECDLP）算法实现的。

数字签名过程如下：

选择一个随机数k作为私钥。

计算公钥K = kG。

计算签名s = k + r n，其中r是随机数，n是椭圆曲线的阶。

将签名s和公钥K发送给接收方。

比特币曲线的属性在比特币系统中发挥着至关重要的作用。通过对比特币曲线的深入理解，有助于我们更好地认识比特币的安全性、可靠性和去中心化特性。